Tetrahedron

Hint
Click or touch on a Platonic solid in the overview to the left. Then change its direction and speed of rotation with the mouse or your finger.
 |
The tetrahedron (greek “tetráedron” = four-sided) is bounded by 4 regular triangles. The faces are bordered by 6 edges of equal length and 4 vertices. 3 triangles meet at each of the vertices. The tetrahedron has the least ratio of volume to surface area. According to Plato it symbolizes dryness or fire. |
 |
The hexahedron (greek “hexáedron” = six-sided) is bounded by 6 squares. The faces are bordered by 12 edges of equal length and 8 vertices. 3 squares meet at each of the vertices. The tetrahedron rests solidly on its base. According to Plato it stands for the stable earth. |
 |
The octahedron (greek “oktáedron” = eight-sided) is bounded by 8 equilateral triangles. The faces are bordered by 8 edges of equal length and 6 vertices. 4 triangles meet at each of the vertices. It can rotate freely when grasped at opposite vertices and symbolizes air. |
 |
The dodecahedron (greek “dodécáedron” = twelve-sided) is bounded by 12 regular pentagons. The faces are bordered by 30 edges of equal length and 20 vertices. 3 pentagons meet at each of the vertices. It represents the universe and, according to Plato, its faces symbolize the 12 signs of the zodiac. |
 |
The icosahedron (greek “eikosáedron” = twenty-sided) is bounded by 20 equilateral triangles. The faces are bordered by 30 edges of equal length and 12 vertices. 5 triangles meet at each of the vertices. It has the highest ratio of volume to surface area and, according to Plato, symbolizes water. |
The solids on this page are controled via JavaScript, but there is a simpler way to animate the solids, too. The Platonic solids can be found as GIF animations to download for free here:
Please note that these GIF animations are intended solely for a specific background color (white or black). If they are displayed against other backgrounds, the result is usually not-too-pretty stair-step artifacts.
My work is published under the terms of the Creative Commons 3.0 Lizenz and may be used freely for private and commercial purposes. I would be glad if reference is made to the author or if a link to this website is posted.
Platonic solids are completely regular solids whose faces are equiangular and equilateral polygons of equal size. An identical number of faces meet at each vertex. Mathematically speaking, the solids are regular polyhedrons (multi-sided), i.e. particularly uniform convex polyhedrons. There are just 5 Platonic solids: tetrahedra, hexahedra, octahedra, dodecahedra and icosahedra.
The oldest man-made Platonic solids are over 4000 years old. Carved in stone balls, they are tetrahedra, hexahedra, octahedra and dodecahedra that were found in different places in Scotland. The first architectural structures based on the octahedron, pyramids, were built at about the same time in Egypt and Central America.
The mathematical laws governing the three Platonic solids tetrahedron, hexahedron, and dodecahedron were first studied about 2500 years ago by the Pythagoreans, a community founded by Pythagoras of Samos (570 - 496 B.C.) dedicated to the exploration of mathematics, astronomy, ethics and religion. A mathematical postulation for the remaining 2 solids, octahedron and icosahedron, as well as proof that exactly 5 Platonic solids exist, was ultimately brought by the Greek mathematician Theaetetus (415 - 396 B.C.).
The Greek philosopher Plato (428 - 348 B.C.) described the solids extensively later on in his book “Timaios” and allotted them to the elements within the Platonic world view. According to his theory the world consists of the 4 basic elements fire, water, air and earth. In turn, these basic elements consist of small, indivisible atoms which, again according to Plato, have the shapes of the Platonic solids. The 4 elements are individually allotted to the solids as follows; the dodecahedron was added later as ‘fifth’ element.
| element | Platonic solid | properties |
|---|---|---|
| fire | tetrahedron | hot and dry |
| water | icosahedron | cold and humid |
| air | octahedron | hot and humid |
| earth | hexahedron | cold and dry |
| universe | dodecahedron |
Before Plato the solids were referred to as “Pythagorean solids”, today they are known under the names “Platonic solids” or “regular polyhedra”.
With the end of ancient times the Platonic solids sank into oblivion for many centuries. It was not until the end of the Middle Ages and the early Renaissance that the solids reappeared in art and science. Leonardo da Vinci and Albrecht Dürer used the solids in their illustrations, and in 1596 Johannes Kepler conceived a solar system that stipulated the orbits of the 6 planets known at the time using the radii of spheres enclosing and enclosed in the Platonic solids.
| Tetrahedron | Hexahedron | Octahedron | Dodecahedron | Icosahedron | |
|---|---|---|---|---|---|
| Volume | 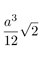 |
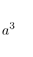 |
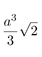 |
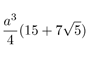 |
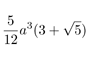 |
| Surface area | 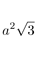 |
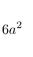 |
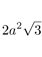 |
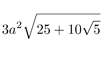 |
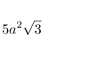 |
| Circumradius | 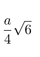 |
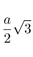 |
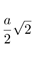 |
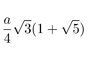 |
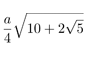 |
| Insphere radius | 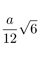 |
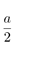 |
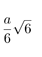 |
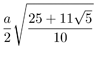 |
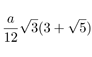 |
Enter a value for the edge length, the volume, the surface area, the circumradius or the insphere radius. The dependent values will then be computed.
| Variable | Tetrahedron | Hexahedron | Octahedron | Dodecahedron | Icosahedron |
|---|---|---|---|---|---|
| Edge length | |||||
| Volume | |||||
| Surface area | |||||
| Circumradius | |||||
| Insphere radius |